[메디컬 세특 칼럼] 로그의 활용 : Log scale
안녕하세요 Recordwriter입니다. 이번 게시글은 수학1 교과 세특 참고자료로 제작한 '로그의 활용 : Log scale' 제목의 세특 칼럼이며 제가 이전에 블로그에 작성한
화학1 완충용액의 원리 : Handerson Hasselbalch Equation과 연관성이 있으므로 필요하시다면 함께 확인하시고 활용하시면 좋을 듯 합니다.
✔️ 과목 : 수학 1
✔️ 학년 : 고2 ~ 고3
✔️ 탐구 주제 : 로그의 활용
1. 탐구 동기
우리는 수학1 교과 수업을 통해 로그가 어떤 것이며, 이를 단순히 계산적인 측면에서 어떻게 처리할 것인지에 대해 집중적으로 배우며 연습하지만 그게 어떤 의미를 가지는 것이며 궁극적으로는 어떻게 활용될 지에 대해서는 생각해본 적이 많지 않다. 지난 탐구에서 완충용액의 원리를 설명하는 Handerson Hasselbalch Equation에 로그가 포함되어 있는 것을 보며 로그라는 수학적 도구가 가지는 실용적 측면에 대하여 그 본질을 탐구해보고 싶은 생각이 들었다.

2. 탐구 내용
① 교과 내용 정리
로그란 어떤 수를 나타내기 위해 고정된 밑을 몇번 곱하여야 하는지를 알려주는 수학적 도구이다. 2를 5번 제곱한 값이 무엇인가?에 대한 답은 지수방정식으로 표현될 수 있는 반면 32는 2를 몇번 곱한 것인가?하는 질문은 로그를 활용해 표현할 수 있다. 이러한 예시에서 우리는 로그와 지수가 역함수의 관계에 있다는 것을 알 수 있다.

로그는 밑과 진수로서 표현되는데, 밑은 1이 아닌 양수여야하며 진수는 항상 양수여야 한다는 조건이 존재한다. 또한 우리는 주로 계산적인 관점에서 로그의 밑과 진수를 어떻게 처리하는지에 대해 주로 배우며 이를 정리하면 아래와 같다.

이처럼 교과 내용을 다시 한번 스스로 정리해보는 것은, 세특에 기재되어야 할 중요한 요소는 아니지만, 해당 탐구가 교과내용의 완전한 이해에서 비롯된 것이며 교과 내용과 큰 관련성을 가진다는 것을 강조하기 위함이다.
② 심화 내용 탐구
로그의 활용적 측면에 대해 복잡하게 파고들기 전에 로그를 취하는 것을 가장 직관적으로 설명해보자. 로그는 큰 수를 간단한 수로 변환 시킨다는 것이 우리에게 가장 와닿는 로그의 본질적 특성이며 이것이 로그 활용의 기본이 된다.
A~D라는 4명의 사람이 각각 100만원, 1억원, 10억원, 12억원이라는 돈을 가지고 있다고 가정해 보자.
✔️ A : 100 만원
✔️ B : 1 억원
✔️ C : 10 억원
✔️ D : 12 억원
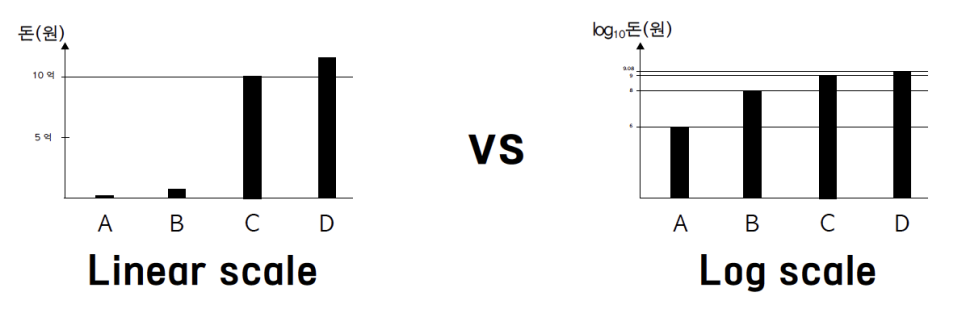
이들이 가진 돈을 하나의 그래프로 표현하고 그 관계에 대해 설명할 수 있을까? 이 과정에서 우리가 당장에 직면하는 문제점은 이처럼 큰 차이를 가지는 수들을 하나의 눈금체계(하나의 축)로 표현하기가 쉽지 않다는 것이다. 그럼에도 축을 지나치게 늘려 어떻게든 하나의 그래프상에 아래와 같이 나타내었다고 하자.
우리가 표나 그래프와 같은 도구를 활용하는 것은 수로 표현되는 데이터를 보다 시각적으로 나타내어 그 관계를 이해하기 쉽게 하기 위해서다. 위 그래프는 그러한 목적에 부합하는가? 이러한 관점에서 두가지 문제를 제기할 수 있다.
문제 ①
100만원(A)과 12억(D)이라는 큰 차이를 가지는 수를 하나의 축 하에 표현하기 위해 축을 지나치게 늘렸고 그 결과 비교적 작은 값인 A와 B는 그래프 상에서 시각적으로 정확히 표현되기가 어렵다.
문제 ②
A와 B는 절대적 금액의 값 차이가 9900만원인 반면 C와 D의 차이는 그 2배 이상인 2억에 해당한다. 이러한 차이는 그래프 상에서 막대의 높이 차이로 그대로 반영되어 나타나는데, 그렇다면 우리는 D는 C보다 훨씬 부자인 반면, A와 B는 재산의 차이가 비교적 적은 것이라 할 수 있는가?
현실적인 관점에서 100만원 하던 주식이 1억원이 된다면 우리는 이를 '대박'이라 표현할 것이다. 분명 이는 10억원이 12억원이 되는 것보다 체감적으로 더 크게 느껴지는 것이지만 절대 값으로 표현된 선형 그래프는 이를 잘 표현하지 못한다.
로그 활용의 실용적 도구
: Log scale
앞서 살펴본 문제의 본질적 원인은, 우리가 비율적 차이보다는 절댓값의 차이로 그래프를 표현하였기 때문이다.
하지만 앞선 예시와 같이 우리의 생활 중에는 절댓값의 차이보다 비율적인 변화가 더 중요한 상황들이 더러 있다. 이러한 문제를 해결하기 위해 우리는 축을 지나치게 늘리는 대신, y축에 밑이 10인 상용로그를 취하는 방식을 취할 수 있다.

y축에 상용로그를 취한 이 그래프는 이전 그래프와 어떤 차이가 있는가? 우선 절대적으로 큰 차이를 가지는 값들을 하나의 축 상에서 적당한 값으로서 나타낼 수 있다. 이는 로그를 취함으로서 큰 값들을 간단한 작은 값들로 변환하였기에 가능한 것이다.
또한, 해당 그래프는 A와 B의 재산 차이가 C와 D의 재산 차이보다 비율적으로 더 크다는 것을 명확히 보여준다. 즉, 로그를 취하는 것은 절대적 값의 차이를 비율적 차이로 전환시키는 것이며 이는 그래프를 통한 보다 직관적 이해를 가능하게 한다.


앞선 그래프 표현 방식을 Linear scale(선형스케일)이라 하며 이는 우리에게 보다 친숙한 방식이다. 반면 축에 log를 취하여 표현하는 방식을 Log scale이라 하는데 이는 값들 사이의 비율적 관계를 명확하게 나타낸다.
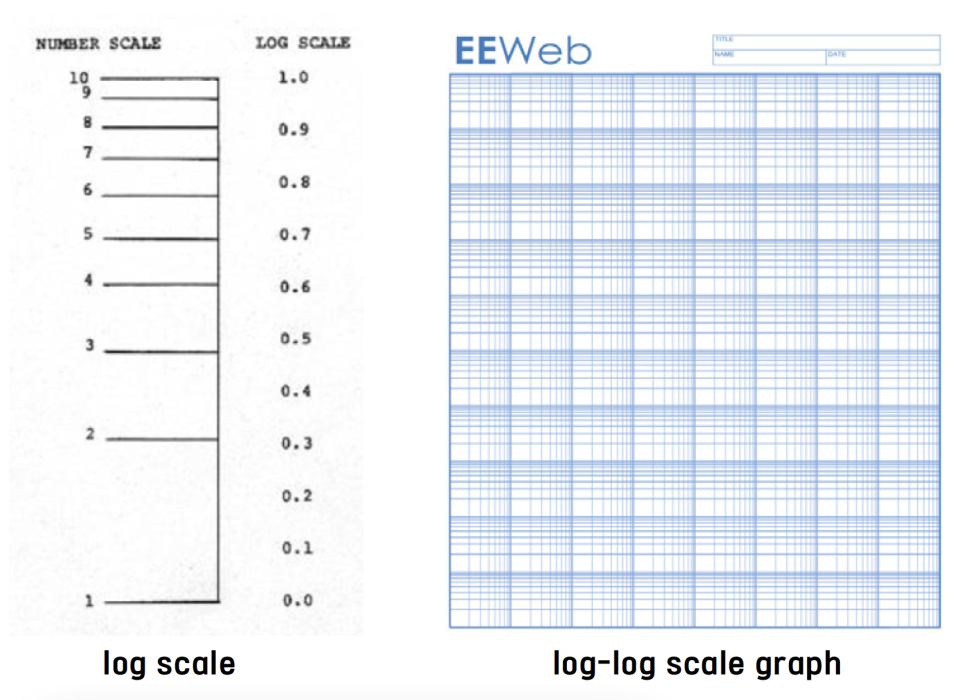
Log scale은 x축과 y축 중 하나에만 로그를 취하여 그래프로 표현하는 semi-log graph, 혹은 x축과 y축 모두에 로그를 취해 표현하는 log-log graph 로 활용되며 이러한 그래프 방식은 자연 과학, 공학 등 여러 과학 분야에서 광범위하게 활용되고 있다.
< log scale의 장점 정리하기 >

3. 진로 연계
앞서 살펴본 것처럼 로그로 표현하는 방식은 다양한 장점을 지니며 따라서 우리 주변의 많은 분야에서 활용되고 있다.

가장 대표적인 예시는 완충용액을 설계하는 과정에서 완충용액의 원리를 설명하는 Handerson-Hasselbalch Equation에 로그가 포함된 것이며 이는 지난 탐구 게시글을 참고하도록 합시다!
https://blog.naver.com/c1c23c/222975086035
4. 결론

텍스트 복사가 가능한 PDF 파일은 아래 블로그를 통해 무료로 다운로드 가능합니다! 감사합니다.
https://blog.naver.com/c1c23c/222979643094
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
ㄷㄷ
-
아버지께서 경제적 독립하라는 눈치를 꽤 주시네요 학과이슈로 삼반 생각있었는데...
-
ㅈㅂㅈㅂㅈㅂㅈㅂㅈㅂㅈㅂㅈㅂㅈㅂㅈㅂㅈㅂ
-
입학처 상담신청 0
여기서 뭐해주는거에요??
-
오르비 첫 글이 이게 될 줄은 몰랐는데.. ㅎ 궁금하신 거 있으시다면 질문 받을게요
-
칸수 떡상 ㅈㅂㅈㅂㅈㅂㅈㅂ
-
나는 사탐을 하고 문과를 가고 싶을 뿐이야 공대에는 관심도 없고 갈 생각도 없었는데...
-
https://seochoedu.or.kr/index.do 서초구에서 원서...
-
인분같은새끼들 0
물론 제 팀원들
-
한의대 0
걍 맘편하게 한의대 가야겠다 치대 안쓸래 원광한 일루와ㅎㅎ
-
필요하신분들은 광클 ㄱㄱ 자세히 들어보진 않았는데 해설할때보니까 방법론은 좋아보였음
-
화장실안에 사람있다고 아직 40%라고 ㅆㅂㄹㅁ
-
평가원 #~#
-
급호감
-
테스트 1
아아
-
예비고3인데요 수능때 생윤사문 하려고 했다가 사문 도표 죽어도 못하겠어서 생윤한지로...
-
고속 대성 다 80프로뜨는데 낙지갑자기 5칸에서 3됨 최상위권대학임 최근3년도컷분석해도 남는 점수임
-
진학사 왜 분석중이라뜨죠
-
변표도 없는데 컨설팅을 어캐함 진짜 2주전인데 그냥 고민하지 말고 물로 내줘....
-
(서울대 합격 / 합격자인증)(스누라이프) 서울대 25학번 단톡방을 소개합니다. 0
안녕하세요. 서울대 커뮤니티 SNULife 오픈챗 준비팀입니다. 서울대 25학번...
-
컴마나 that으로 세줄 넘어가는 문장은 축적이 안되는 느낌이 들고 대충 수식하는...
-
집으로
-
농어촌 버리고 학교 잘못 선택한 죄 재수로 죗값은 치르는중
-
올해꺼가 베이스/어드밴스드로 나눠져잇는데 그냥 올해꺼듣는게 나을까요
-
변표좀 까라.. 2
원서 접수 2주도 안남았는데 ㅋㅋ
-
망했네
-
[수학] 조건해석을 쉽게 하는 법과 실력을 키우는 방법 +강좌소개 2
안녕하세요 오르비 수학강사 이대은입니다. 오늘 글은...
-
이제는 진짜 뇌절이네..
-
작년 입시 뽕을 봐서 그런거임 미적이랑 확통이 11-12점이 차이가 나고 고대는...
-
진짜로요
-
해결됐습니다. 10
고뇌 끝에 이 문제를 어떻게 푸는지 드디어 알아냈습니다. 그 내용은 다음 만화에...
-
심심한데 질문받음 11
아무거나질문하시면받습니다
-
굿노트나 사진촬영 이런거 다 막혀있늠? 태블릿 용량은 어느정도됨?
-
라고 하면 안되겠죠?
-
문과는 사탐만 이과는 과탐만 받게 하면 해결되는 거 아님?
-
ㄹㅇ 정신병 올거같음 제발 월요일엔 좀 빠져라....
-
라고 이주호가 말하네요
-
삼수 0
재수때 과정은 차치하고 결과가 많이 오르지않았다면 삼수도 사치라 생각함?
-
그렇게 간절히 반수할곳이 필요한건지 뭐 작년 고대처럼 문과에 과탐변표 4점씩 이득봐야 직성 풀리나
-
내신도 끝낫고.. 개념의 나비효과 책 올때까지만 놀려고했는데 아직 안와서 폐인...
-
궁금한게있사옵니다
-
10대라면 참여 가능! 문화상품권 받아가자(오늘까지!)✨ 0
설문조사 참여 많이 안해주셔서 문상 받을 확률 높습니다! 참여 부탁드립니다!!...
-
물변 이득 0
99 80 물변이라 이득인거같긴한데 유불리가 바뀌진않앗네..쩝
-
안녕하세요 고3 남자 현역입니다. (중3때까지 축구 선수 였음) 두 곳을...



































































첫번째 댓글의 주인공이 되어보세요.