"Chapter. 0 - 함수의 연속"
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

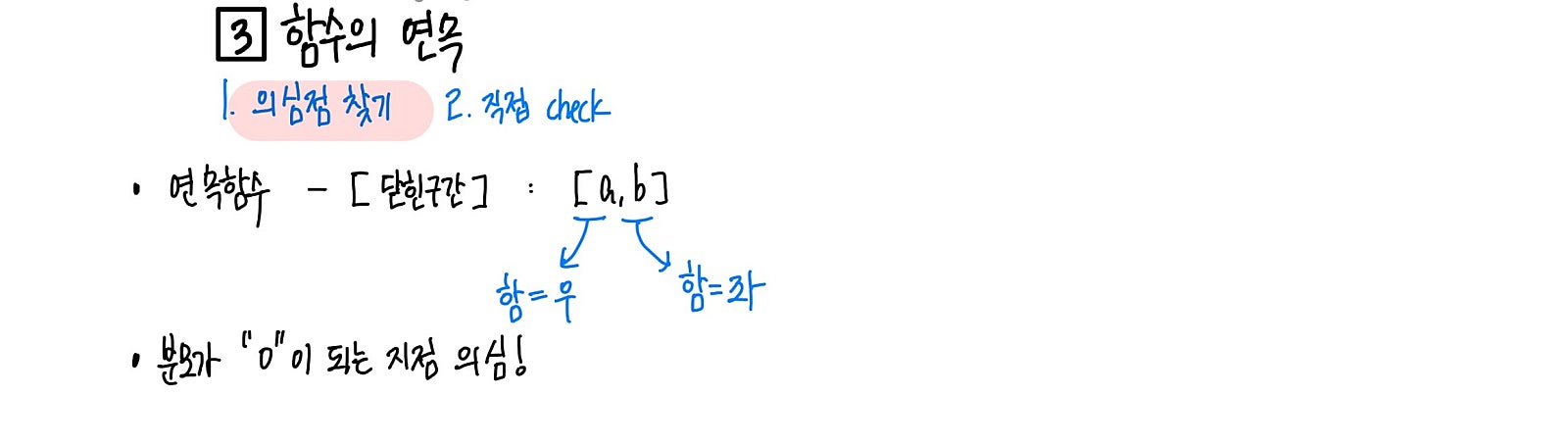
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
ㄷㄷ 7
-
어머 예쁘다. 0
오늘로써 오르비의 정수를 깨달았다 정수 약탈자.
-
오...
-
싶네요 사과도 안하는 건 좀 의아함 후기들 보면 해주는 거에 비해 많이 받으시는 거...
-
흠
-
카페인 마시고 잠 별로 안 자서 그런가 머리가 잘 안 돌아가네
-
나한테 싸움거는거야?
-
오 12
오오
-
단돈 5만덕
-
무안공항 '로컬라이저 개량' 당시 공항공사 사장 숨진 채 발견 2
(서울=연합뉴스) 이동환 정윤주 기자 = 경찰대학장 출신의 정치인 손창완 전...
-
https://orbi.kr/00071495666
-
비문학 노베이슨데 이 두개 중에 뭐 사야하는건가요???
-
최애곡까지 겹침 다시 청혼...해야겠지?
-
24 (집모) 49344 25 6모 43311 25 9모 44312 25 수능...
-
요즘 취업 새내기 때부터 차근차근 대비하는 법 [숭실대 꿀팁] 0
대학커뮤니티 노크에서 선발한 숭실대 선배가 오르비에 있는 예비 숭실대생, 숭실대...
-
아직까지 안 한 대학들은 그럴 능력이 안 되거나 수험생의 고통을 즐기는 사이코 둘...
-
분명히 영상에서는 “선관위 의혹해소“만 이야기 했는데 민주당에서 발끈하네요? 흠..
-
고3인데 유형문제집으로 마플시너지 비추인가요? 그냥 알피엠이랑 김기현 킥오프만 하고...
-
이게 왜 사지는데? ㅠㅠ 버그아냐?
-
가격이 정상화 될것.
-
아저씨는 없고요 외대 중국어문화학과 ㅈ베ㅏㄹ...
-
저는 올검이 예쁜거같은데 몇몇대학 빼곤 못본 듯
-
지문읽을때 3에서4분 정도 걸리는데 읽는시간에 더 써야되나? 6 7분 이렇게 읽으면...
-
이런김에 0
아이즈원 레어 다 모아보자
-
히히
-
레어 개수제한은 없는데 10
표시는 4개만 되는거임? 인하대 레어가 안보이네
-
경희대 조발ㄷ 4
6시에 발표 정확히 나나요 아니면 몇시간이라도 일찍 발표해주나요
-
Chill guy만 있는게 너무 chill한 것 같아서요.
-
나 순애야 30
한놈만 파 한눈 안 팔아 자신 잇어 그러니까 아무나 내 님이 되어줘.. ㅠㅠ
-
김동욱 언매 체크메이트 들었는데 다음으로 본바탕 들으면 되나요? 그 다음으로 뭐...
-
칼럼을 쓰기에는 13
글 실력이 보잘 거 없구나 쩝
-
몰카 찍게 넝담이고 할거ㅜ잇음
-
레선족 척결 1
다섯글자에 ○○○
-
좋겠어요..
-
손해볼일이 없는거임?
-
졸려 자고 싶어 6
-
학력보나요..?
-
안녕하세요 '지구과학 최단기간 고정 1등급만들기' 저자 발로탱이입니다. 지난 1년간...
-
정신 나가기
-
굿
-
ㅈㄱㄴ
-
2025kice ㄱㄱ
-
레테크펀드에 투자하세요 오늘 새벽 or 원하실 때까지 레테크해서 (투자하신...
-
이런스타일 좋아합니다...
-
팀원들이 예전팀원하고 능력치 자체가 다르니까 힘드네.. 젠지가 돈만 좀더 많았더라면..
-
이 글에 덕코뿌리면 스나합함
-
(1/3)x^2이 아니구나
-
어제 4만 3천덕 -> 오늘 14만덕 돌파함 결론 -> 레테크하라!















































